值得深思的一道算法题LC4

4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n))

解法一

思路

最最简单粗暴的想法，将两个数组进行合并，两个有序数组的合并是属于「归并排序」中的一个环节，然后返回结果即可。

实现

class Solution {
    public static final int MAXN = 2010;
    public static final int[] nums = new int[MAXN];
    
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        
        if(m == 0) {
            return (n & 1) == 0 ? (nums2[n/2-1] + nums2[n/2]) / 2.0 : nums2[n/2];
        }
        if(n == 0) {
            return (m & 1) == 0 ? (nums1[m/2-1] + nums1[m/2]) / 2.0 : nums1[m/2];
        }

        // int[] nums = new int[m + n];
        int idx = 0, i = 0, j = 0;
        while(idx != nums.length) {
            if(i == m) {
                while(j != n) nums[idx++] = nums2[j++];
                break;
            }
            if(j == n) {
                while(i != m) nums[idx++] = nums1[i++];
                break;
            }
            if(nums1[i] < nums2[j]) {
                nums[idx++] = nums1[i++];
            } else {
                nums[idx++] = nums2[j++];
            }
        }
        return (idx & 1) == 0 ? (nums[idx/2-1] + nums[idx/2]) / 2.0 : nums[idx/2];
    }
}

• 时间复杂度：O(m+n)
• 空间复杂度：O(m+n)

解法二

思路

解法一是直接将两个数组进行了合并，但其实不需要，只需要找到中位数的位置即可。

1）针对于奇数的情况：需要知道 (len+1) / 2 位置上的数字，也就是需要遍历 len/2 + 1个数字；

2）针对于偶数的情况：需要知道 len/2 和 len/2 + 1 位置上的数字，还是需要遍历 len/2 + 1 个数字。

=> 奇偶数的情况都是需要遍历 len/2 + 1 个数字。

返回答案的时候，奇数情况直接返回，偶数情况需要保留上一轮的结果，然后和这一轮的结果求和取平均。

实现

class Solution {
    public double findMedianSortedArrays(int[] a, int[] b) {
        int m = a.length, n = b.length;
        int len = m + n;
        int l = -1, r = -1, as = 0, bs = 0; // a/b start pointer
        // 无论奇偶，都需要循环 len/2+1 次
        for(int i = 0; i <= len / 2; i++) { 
            l = r; // l 保留上一次的结果，因为偶数需要两次的取平均
            if(as < m && (bs >= n || a[as] < b[bs])) {
                r = a[as++];
            } else {
                r = b[bs++];
            }
        }
        return (len & 1) == 0 ? (l + r) / 2.0 : r;
    }
}

• 时间复杂度：O(m+n)
• 空间复杂度：O(1)

解法三

思路

解法一和解法二的时间复杂度都没有达到题目的要求 O(log(m+n))。

时间复杂度要求到达 log 级别，很明显需要我们使用到二分的方法。题目要求的是中位数，也就是「求第k小数」的一种特殊情况。

解法二中，一轮循环相当于去除一个不满足题意的值，也就是说这种方法是一个数一个数的排除。由于数组是有序的，我们完全可以一次排除掉一半的数字，假设现在要找第k小的数，我们可以每轮循环排除掉k/2个数字。

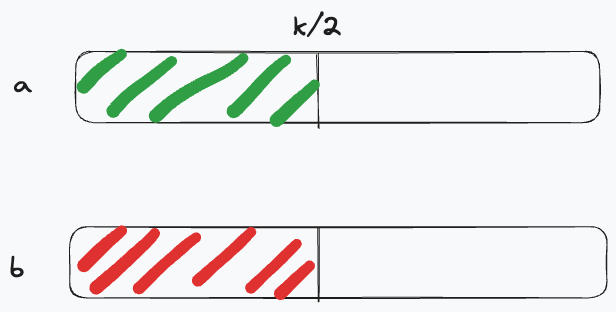
如果 a[k/2] < b[k/2]，那么可以直接排除掉 a[0...k/2]的元素了，因为 a 中比 a[k/2] 小的数有 k/2-1个，现在假设 b[0...k/2-1]都小于 a[k/2]，那么一共有 k/2-1+k/2-1 = k-2个数比 a[k/2] 小，也就是说 a[k/2] 最大是第 k-1 小的数，因此比 a[k/2] 小的数更不可能是第 k 小的数了，所以可以将它们排除。

数组中剩下的部分和原问题类似，可以使用递归来解决。

注意：

1）因为每次都是取 k/2 的数进行比较，那么可能会遇到数组长度小于 k/2的情况，这种情况直接取数组中的最后一个元素，即一次性排除掉整个数组；

2）当某一个数组在递归树中为空时，可以直接返回结果；

小 trick：奇数和偶数情况都可以取 (m+n+1)/2 和 (m+n+2)/2 的数字来取平均，因为在奇数情况下二者相等。

实现

class Solution {
    public double findMedianSortedArrays(int[] a, int[] b) {
        int m = a.length, n = b.length;
        // 奇数情况下 l == r
        int l = (m + n + 1) / 2, r = (m + n + 2) / 2;
        return (findKth(a, 0, m - 1, b, 0, n - 1, l)
                + findKth(a, 0, m - 1, b, 0, n - 1, r)) / 2.0;
    }

    // a[al...ar], b[bl...br]
    public static int findKth(int[] a, int al, int ar, int[] b, int bl, int br, int k) {
        int la = ar - al + 1, lb = br - bl + 1;

        // 保持 la <= lb, 这样空数组一定是 a
        if(la > lb) {
            return findKth(b, bl, br, a, al, ar, k);
        }
        // base case
        if(la == 0) {
            return b[bl + k - 1];
        }
        if(k == 1) { // a, b 都不为空
            return Math.min(a[al], b[bl]);
        }

        // 求中间位置，同时需要防止数组长度小于 k/2, 如果小于，取最后一个元素
        int ai = al + Math.min(la, k / 2) - 1;
        int bi = bl + Math.min(lb, k / 2) - 1;
        if(a[ai] > b[bi]) { // 去除 b[bl...bi]
            // 下一轮找第 k-(bi-bl+1) 的数字 
            return findKth(a, al, ar, b, bi + 1, br, k - (bi - bl + 1)); 
        } else { // 去除 a[al...ai]
            return findKth(a, ai + 1, ar, b, bl, br, k - (ai - al + 1));
        }
    }
}

• 时间复杂度：O(log(m+n))
• 空间复杂度：O(1)，因为是尾递归

解法四

LC-4

思路

实现