next-node-of-binary-tree

找出 二叉树的下一个节点？

这是一道来自于 《剑指 Offer》 的题目，题目信息：

给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示。

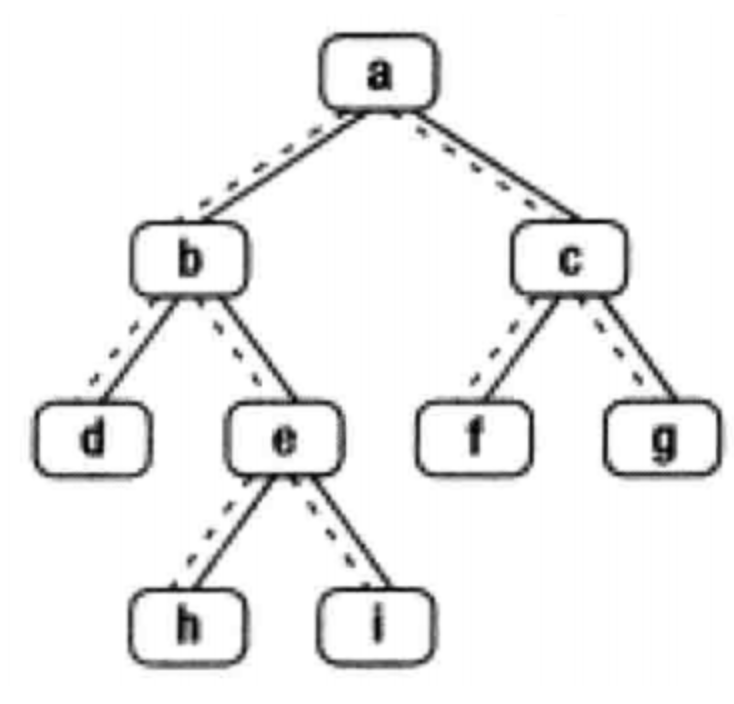
起初第一眼看到这道题，感觉不就是中序遍历下整棵树，然后就能找到了嘛，诶呀，轻轻松松~

但是呢，事情发生了微妙的转变，是因为根本就不知道树的根节点，没法遍历，啊~

import java.util.*;
/*
public class TreeLinkNode {
    int val;
    TreeLinkNode left = null;
    TreeLinkNode right = null;
    TreeLinkNode next = null;

    TreeLinkNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        // write your code here
    }
}

那这就只能根据中序遍历的特点来做题了啊。

简单回顾下中序遍历：先递归访问左子树，再访问自身，再递归访问右子树。简单记为左中右。那么就可以考虑下使用到这个特性了。啊哈，坐好车，我们要出发了~

思考如下的一种情况：

如果一个节点有右子树，那么该节点的下一个节点就是它的右子树的最左子结点了。举个例子，上图中的节点b的下一个节点是节点h，节点a的下一个节点是f。

这种情况的代码实现：

// 情况一：pNode 右子树不为空，下一个节点即为右子树的最左节点
TreeLinkNode pNext = null;
TreeLinkNode right = pNode.right;
while(right.left != null) 
    right = right.left;
pNext = right; // pNext 即为下一个节点

接着来思考：

如果一个节点没有右子树呢？如果该节点是其父节点的左子结点，那么它的下一个节点就是它的父节点了。举个例子，上图中的节点d的下一个节点是节点b，节点f的下一个节点是节点c。

那如果一个节点既没有右子树，并且它还是其父节点的右子节点呢？这种情形就比较复杂了，我们需要将这种情况化归到上述的的情况，也就是该节点是其父节点的左子结点的情况。如何做到呢？我们可以沿着指向父节点的指针一直向上遍历，直到找到一个节点，该节点是它父节点的左子结点。如果我们找到了这样的节点，那么这个节点的父节点就是我们要找的下一个节点。

我们来看一个例子，找到上图中节点i的下一个节点，我们可以沿着指向父节点的指针，先到达节点e，但是节点e是它父节点b的右节点，继续向上遍历到达节点b，节点b是它父节点a的左子结点，因此节点b的父节点a就是节点i的下一个节点。同理我们可以找到节点g的下一个节点，结果为空，也就是节点g没有下一个节点。

上述过程需要对二叉树中序遍历有充分的理解。

这两种情况的代码实现：

// 情况二：pNode 右子树为空，但是其父节点的左节点，下一个节点即为其父节点
// 情况三：pNode 右子树为空，且是其父节点的右节点，这种情况需要顺着父节点一路往上遍历
// 直到找到一个节点，该节点是其父节点的左节点，下一个节点即为该节点的父节点 => 归纳为情况二
TreeLinkNode pNext = null;
TreeLinkNode cur = pNode, next = pNode.next;
while(next != null && cur == next.right) {
    cur = next;
    next = next.next;
}
pNext = next; // pNext 即为下一个节点

至此，我们就分析完了这道题。这道题还是需要对二叉树中序遍历有深入的理解才能够实现的。平时我们可以多画画图，举一些例子，找出规律，来帮助我们解题。

完整代码：

import java.util.*;
/*
public class TreeLinkNode {
    int val;
    TreeLinkNode left = null;
    TreeLinkNode right = null;
    TreeLinkNode next = null;

    TreeLinkNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        // 情况一：pNode 右子树不为空，下一个节点即为右子树的最左节点
        // 情况二：pNode 右子树为空，但是其父节点的左节点，下一个节点即为其父节点
        // 情况三：pNode 右子树为空，且是其父节点的右节点，这种情况需要顺着父节点一路往上遍历
        // 直到找到一个节点，该节点是其父节点的左节点，下一个节点即为该节点的父节点 => 归纳为情况二
        TreeLinkNode pNext = null;
        if(pNode.right != null) {
            TreeLinkNode right = pNode.right;
            while(right.left != null) 
                right = right.left;
            pNext = right;
        } else if(pNode.next != null) {
            TreeLinkNode cur = pNode, next = pNode.next;
            while(next != null && cur == next.right) {
                cur = next;
                next = next.next;
            }
            pNext = next;
        }
        return pNext;
    }
}