问题
有n件物品,一个最多能背重量为w的背包,第i件物品的重量是weight[i],价值是value[i]。
每件物品只能使用一次 。
问:将那些物品装入背包里物品价值总和最大?
暴力解法
思路
每件物品的状态:选或者不选。
=> 使用回溯法 搜索出所有的情况。时间复杂度\(O(2^n)\) ,n为物品数量。
示例代码:
【Java】
public class ZeroOneKnapsack { private int ans; public int zeroOneKnapsack (int n, int w, int [] weight, int [] value) { ans = 0 ; dfs(n - 1 , 0 , 0 , w, weight, value); return ans; } private void dfs (int i, int curWeight, int curValue, int w, int [] weight, int [] value) { if (curWeight > w) { return ; } if (i < 0 ) { ans = Math.max(ans, curValue); return ; } dfs(i - 1 , curWeight, curValue, w, weight, value); dfs(i - 1 , curWeight + weight[i], curValue + value[i], w, weight, value); } } public class Main { public static void main (String[] args) { ZeroOneKnapsack knapsack = new ZeroOneKnapsack (); int n = 3 , w = 5 ; int [] weight = { 2 , 3 , 1 }; int [] value = { 4 , 5 , 2 }; int ans = knapsack.zeroOneKnapsack(n, w, weight, value); System.out.println(ans); } }
【Python】
class Knapsack : def zero_one_knapsack (self, n:int , w:int , weight:list , value:list ) -> int : ans = 0 def dfs (i: int , cur_weight = 0 , cur_value = 0 )-> int : if cur_weight > w: return if i == 0 : nonlocal ans ans = max (ans, cur_value) return dfs(i - 1 , cur_weight, cur_value) dfs(i - 1 , cur_weight + weight[i - 1 ], cur_value + value[i - 1 ]) dfs(n - 1 ) return ans knapsack = Knapsack() n = 3 w = 5 weight = [2 , 3 , 1 ] value = [4 , 5 , 2 ] ans = knapsack.zero_one_knapsack(n, w, weight, value) print (ans)
二维DP数组
数据示例:
1)背包最大重量为4
2)物品为:
物品序号
重量
价值
0
1
15
1
3
20
2
4
30
思路
01背包写法之一是使用二维数组。
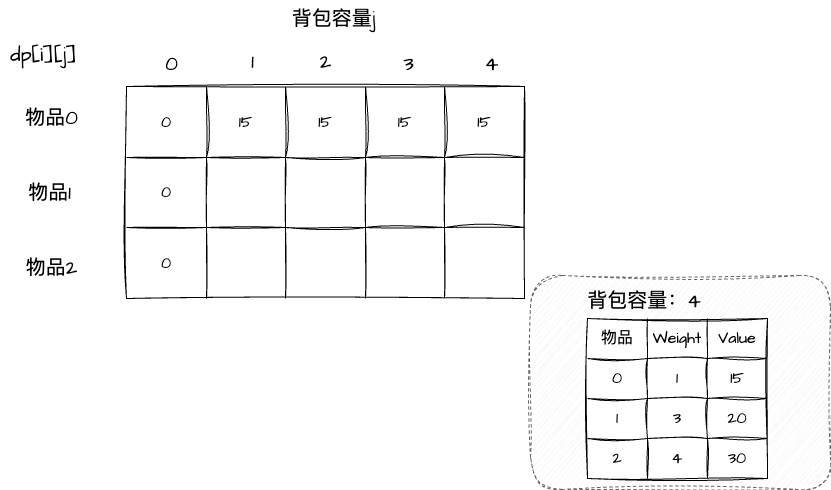
定义一个二维数组dp,dp[i][j]的含义是从下标范围为[0, i]的物品数组中取一件物品,放入容量为j的背包所能取得的的最大价值 。
根据数组的定义可以得知有两个方向可以推导出:dp[i][j]
不放物品i :由dp[i - 1][j]推导出,即背包容量为j时,不放物品i所得到的最大价值,此时dp[i][j] = dp[i - 1][j]放物品i :由dp[i - 1][j - weight[i]]推导出,dp[i - 1][j - weight[i]]表示背包容量为j - weight[i]时放入物品i得到的最大价值,此时dp[i][j] = dp[i - 1][j - wieght[i]] + value[i]
=>
递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
接下来讨论DP数组的初始化,只有初始化了,递推公式才有意义,依旧是从数组的定义出发:
如果背包容量j = 0,即dp[i][0],此时无论选取哪些物品,所得到的最大价值一定是0
根据递推公式可以得到,i的状态是从i - 1推导出来的,因此i = 0一定要初始化,即dp[0][j],存放物品0。各个容量的背包所能存放的最大价值,此处需要分情况讨论:
j < weight[0]时,dp[0][j] = 0,因为背包容量不能放下物品0j >= weight[0]时,dp[0][j] = value[0],此时背包容量足够放下物品0
接下来就是确定遍历顺序,此处有两种选择:
先遍历背包容量再遍历物品
先遍历物品再遍历背包容量
给出结论:对于二维DP数组01背包,先遍历哪个都可以,但是先遍历物品更好理解。
为什么呢?关键理解递推的本质和递推的方向
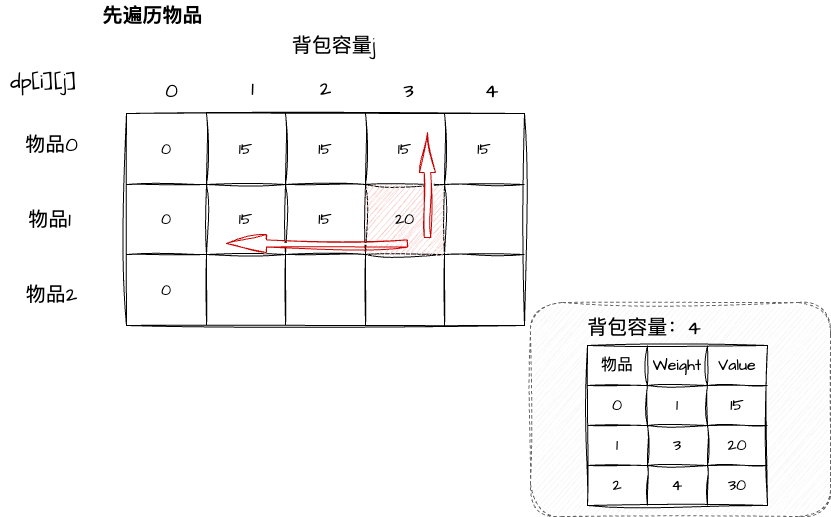
再看一遍递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]),可以看出dp[i][j]是依赖dp[i - 1][j]和dp[i - 1][j - weight[i]]的,这两个值在dp[i][j]的左上角方向(包括正上方方向)。
那么先遍历物品,随后遍历背包容量的过程:
先遍历背包容量,再遍历物品的过程:
=>
遍历次序不同,但是dp[i][j]需要的数据是从左上角来的,不影响dp[i][j]的推导
实际上背包问题里,两个for循环的先后次序是非常有讲究的,理解遍历顺序其实比理解推导公式难度要大
最后来看下这个数据例子下的dp数组的结果
最终的结果是dp[2][4] = 35
示例代码
【Python】
class Knapsack : def zero_one_knapsack (self, w: int , weight: list , value: list ) -> int : n = len (weight) dp = [[0 ] * (w + 1 ) for _ in range (n)] for j in range (weight[0 ], w + 1 ): dp[0 ][j] = value[0 ] for i in range (1 , n): for j in range (w + 1 ): if j < weight[i]: dp[i][j] = dp[i - 1 ][j] else : dp[i][j] = max (dp[i - 1 ][j], dp[i - 1 ] [j - weight[i]] + value[i]) return dp[n - 1 ][w] knapsack = Knapsack() w = 4 weight = [1 , 3 , 4 ] value = [15 , 20 , 30 ] ans = knapsack.zero_one_knapsack(w, weight, value) print (ans)
【Java】
public class ZeroOneKnapsack { public int zeroOneKnapsack (int bagSize, int [] weight, int [] value) { int n = weight.length; int [][] dp = new int [n][bagSize + 1 ]; for (int j = weight[0 ]; j < bagSize; j++) dp[0 ][j] = value[0 ]; for (int i = 1 ; i < n; i++) { for (int j = 1 ; j <= bagSize; j++) { if (j < weight[i]) dp[i][j] = dp[i - 1 ][j]; else dp[i][j] = Math.max(dp[i - 1 ][j], dp[i - 1 ][j - weight[i]] + value[i]); } } return dp[n - 1 ][bagSize]; } public static void main (String[] args) { int [] weight = { 1 , 3 , 4 }; int [] value = { 15 , 20 , 30 }; int bagSize = 4 ; int ans = new ZeroOneKnapsack ().zeroOneKnapsack(bagSize, weight, value); System.out.println(ans); } }
一维DP数组
滚动数组:满足条件的上一层级可以重复利用,直接拷贝到当前层。
背包问题,状态都可以进行压缩。
二维DP数组dp[i][j]含义是从下标范围为[0, i]的物品数组中取一件物品,放入容量为j的背包所能取得的的最大价值,递推公式是dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。
如果在递推的过程中,可以把dp[i - 1]层级拷贝到dp[i]上,表达式就可以转换成dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]),那么就可以使用一个一维数组来存储了,即dp[j],递推公式转变成dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。
那么,定义一维数组dp[j],含义是背包容量为j的背包可以得到的最大价值 。
递推公式就是dp[j] = max(dp[j], dp[j - weight[i]] + value[i]):
dp[j]:不放物品i,相当于dp[i - 1][j]dp[j - weight[i]]:放入物品i,相当于dp[i][j - weight[i]]
接下来就是初始化环节:
关于初始化,一定要和dp数组的定义吻合,否则到递推公式时,逻辑只会混乱
dp[0] = 0:容量为0的背包所能得到的最大容量就是0其余非0下标初始化成0就可以了,这样才可以让dp数组在递推过程中取得的是最大的价值,而不是被初始值覆盖了(如果价值有负数,就可以初始化成最小的负数)
接下来就是最重要的确定遍历顺序的环节:
先给出代码
for (int i = 0 ; i < weight.length; i++) { for (int j = bagWeight; j >= weight[i]; j--) { dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }
可以看出,这里和二维dp数组的写法中遍历背包容量的顺序是不一样的,此处是倒序遍历背包容量,二维数组的时候是顺序遍历背包容量。原因是倒序遍历保证了物品i只被放入一次 。
此处顺序遍历背包容量,物品0就会被重复放入多次。
【栗子🌰】
dp[1 ] = dp[1 - weight[0 ]] + value[0 ]; dp[2 ] = dp[2 - weight[0 ]] + value[0 ];
此时dp[2] = 30 => 物品0 被放入了两次。
如果是倒序遍历:
dp[2 ] = dp[2 - weight[0 ]] + value[0 ]; dp[1 ] = dp[1 - weight[0 ]] + value[0 ];
=>
倒序遍历,每次得到的状态就不会和之前的状态重合,就能保证每种物品只被选取一次
二维dp数组不需要倒序是因为二维dp数组中dp[i][j]是通过上一层dp[i - 1][j]推导得出的,本层级不会被覆盖。
除此之外,必须选择先遍历物品再遍历背包容量 ,因为一维dp数组中,背包容量必须是倒序遍历的,那么如果先遍历背包,每个dp[j]就只会放入一个物品,即背包中只会放入一个物品。
倒序遍历的本质原因 :本质上还是对一个二维数组的遍历,并且二维数组右下角的值依赖左上角的值,因此需要左边的值在计算的时候依然是上一层的,那么就需要从右向左倒序遍历。
最后还是来看下一维dp数组最后的结果:
示例代码
【Python】
class Knapsack : def zero_one_knapsack (self, bag_size: int , weight: list, value: list) -> int : n = len(weight) # 二维数组 dp = [0 ] * (bag_size + 1 ) # 先遍历物品,再倒序遍历背包容量 for i in range (n) : for j in range (bag_size, weight[i] - 1 , -1 ) : dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) return dp[bag_size] knapsack = Knapsack() bag_size = 4 weight = [1 , 3 , 4 ] value = [15 , 20 , 30 ] ans = knapsack.zero_one_knapsack(bag_size, weight, value) print(ans)
【Java】
public class ZeroOneKnapsack { public int zeroOneKnapsack (int bagSize, int [] weight, int [] value) { int n = weight.length; int [] dp = new int [bagSize + 1 ]; for (int i = 0 ; i < n; i++) { for (int j = bagSize; j >= weight[i]; j--) { dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); } } return dp[bagSize]; } public static void main (String[] args) { int [] weight = { 1 , 3 , 4 }; int [] value = { 15 , 20 , 30 }; int bagSize = 4 ; int ans = new ZeroOneKnapsack ().zeroOneKnapsack(bagSize, weight, value); System.out.println(ans); } }